
5次方程式が解けないことの直感的説明
Home > めもらんだむ > 5次方程式が解けないことの直感的説明
5次方程式には解の公式が存在しない。そうはいっても、(代数学の基本定理により)5次方程式には解が5個あるに決まっているのだから、そんなバカなことがあるわけない、と思うかもしれない。
でも、一般の5次方程式に解の公式が存在しそうにないことを納得するのは、実はそんなに難しくはない。そもそも、高次方程式の解が書き表せることのほうが奇跡に近いのだから。
「解の公式が存在する」ということは、方程式の係数に対して、加減乗除とベキ根(n乗根、ただしnは素数と考えてよい)を有限回作用させることでそれぞれの解が書き表せるということだ。
例えば、3次方程式
x3 + ax2 + bx + c = 0
を考えてみよう。3個の解を x1, x2, x3 とすると、解と係数の関係から、
-a = x1 + x2 + x3 (1)
b = x1x2 + x2x3 + x3x1 (1')
-c = x1x2x3 (1")
が成立する。方程式にとっては3個の解に「個性」はないから、どれが x1 でどれが x2 でどれが x3 でも構わない。従って、x1, x2, x3 の値をどのように入れ替えても(置換しても)、(1)~(1")の式は成立する。3つの元に対して、可能な置換は 3! = 6通りある。このように、どう置換しても値が変わらない式を対称式という。
3個の解は互いに何の関係もない独立したものなのに、方程式の中では、3個の解は分かちがたく結びついた形で表現されているのだ。
これを「x1 =(a, b, c の式)」の形として表すためには、この3個の解の間の結びつきをほぐさなければならない。
対称式同士でいくら加減乗除を行っても、つまり、方程式の係数 a, b, c を加減乗除を使ってどうこねくり回しても、対称式しか出てこない。対称式のもつ対称性を分解するためには、ベキ根の助けが必要になってくる。
2次方程式 x2 + ax + b = 0 の解の公式は、
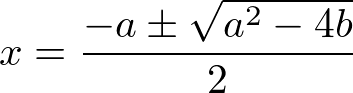
である。この2次方程式の解を x1, x2 とすると、根号の中身は
a2 – 4b = (x1 + x2)2 – 4x1x2 = (x1 - x2)2 (2)
となる。(2)は、x1 と x2 の入れ替え(置換)に対して不変である。
ところが、平方根をとると、y1 = x1 – x2 と y2 = x2 – x1 という2つの値が出てくる。これらの値は、次のような性質をもっている:
y2 は y1 の x1 と x2 を置換したものになっている y2 は y1 に、1の平方根(のうち、1でないもの)を掛けた値になっている(つまり、y2 = -y1)
そのため、x1 – x2 は x1 と x2 の置換によって値が変わるのに、2乗すると対称式になるのだ。
次に3次方程式を考えてみよう。(2)の右辺と同様に、
{(x1 – x2)(x2 – x3)(x3 – x1)}2 (3)
という式を考える。これは x1, x2, x3 をどのように置換しても値が変わらないから、対称式である。
しかし、平方根をとった
(x1 – x2)(x2 – x3)(x3 – x1) (4)
という式では、x1 と x2 の入れ替え(置換)によって符号が変わるようになる。x1 と x3、x2 と x3 のペアで入れ替えを行っても同様である。
ただし(4)は、(x1, x2, x3) を (x2, x3, x1) あるいは (x3, x1, x2) と巡回的に置換しても値が変わらない(このような置換を巡回置換という)。従って、恒等置換も含めて、(4)の値を変えないような置換は3種類ある。最初に6種類あった置換を、平方根をとることで3種類に減らすことができた。
次に
(x1+x2ω+x3ω2)3 (5)
という式を考えてみよう。ここで、ωは1の3乗根(のうち、1でないもの)である。この式もまた、(x2, x3, x1) および (x3, x1, x2) という巡回置換に対して不変である(ω3 = 1に注意)。従って(5)は、(4)と対称式 a~c に加減乗除を施すことで作り出すことができる(証明が必要だが)。
(5)の3乗根をとると、
y1 = x1 + x2ω + x3ω2
y2 = x2 + x3ω + x1ω2
y3 = x3 + x1ω + x2ω2
という3個の値が出てくる。これらの値は、
y2 および y3 は、y1 に、それぞれ巡回置換 (x2, x3, x1) および (x3, x1, x2) を施すことによって得られる y1 = y2ω かつ y2 = y3ω
という性質をもっている。そのため、y1, y2, y3 はどんな置換に対しても不変でないのに、3乗すると巡回置換に対して不変になるのだ。どんな置換に対しても不変でないような数が得られれば、それに適当な加減乗除を施すことで x1, x2, x3 の値を得ることができる。
以上のことから、3次方程式を解くためには、まず平方根をとり、次に3乗根をとる必要があるということが分かる。
実際、カルダーノの公式によれば、3次方程式
x3 + px + q = 0
(一般性を失わずに x2 の係数が0になるように変形できる)の解の一つは、
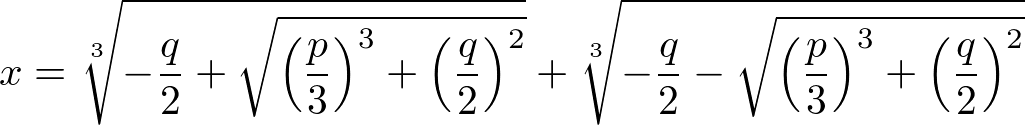
である。
4次方程式になると、解 x1, x2, x3, x4 の可能な置換は 4! = 24通りもある。しかし、4 = 22という特殊性のおかげで、解を2個ずつのペアにすることにより、24通りの置換をうまく分解していくことができる。
たとえば x1x2 + x3x4 という式を考えると、これは24通りの置換に対して、3通りの異なる値をとる。従って、4次方程式の解法は、3次方程式を解くことに帰着されるのである。
ところが5次方程式ともなると、5個の係数 a, b, c, d, e の中に閉じ込められた5個の解 x1, x2, x3, x4, x5 の結びつきはいよいよ強固になり、どうやってもほぐすことができなくなる。
(4)を5変数に拡張した式を考えれば、この場合も、x1~x5の任意のペア同士の奇数回の入れ替え(奇置換)によって符号が変わるようにできる。従って、5!=120通りの置換を、60通りにまで減らすことができる。問題はこの後である。
元が3個の場合は、x1, x2, x3 の巡回置換によって値が変わっても、その巡回置換を3回繰り返す(3乗する)ことで値を不変にすることが可能だった。だから、3乗根をとることで、値を変えない置換の数を減らすことができた。
しかし元が5個ある場合、「x1, x2, x3 の巡回置換と x3, x4, x5 の巡回置換をp回(p:素数)繰り返した結果の値が不変であれば、1回だけ行ったときの値も不変である」ことが(比較的容易に)証明できる。ということはつまり、a~eという対称式から出発した場合、これに加減乗除とベキ根をどう作用させても、値を不変にする置換の数を60通りよりも少なくはできないということだ。
よって、5次方程式の解は加減乗除とベキ根では表せない。証明終わり。■
ただし、数学的に厳密な議論をするためには、加減乗除とベキ根を何回繰り返しても、その結果は複素数の世界からはみ出ない、ということを証明する必要がある(アーベルの補題)。解が複素数であることは保証されているのだから、これは当たり前のような気がする。
しかし、3次という小さな次数の方程式でさえ、たとえすべての解が実数であったとしても、その解を書き表すためには ω (= (-1 + √-3)/2) という実数の外側にある副次的な数が必要になってくるのだ。アーベルの補題は、解の公式が存在するとしたら、途中経過も含めて、加減乗除とベキ根によって作られる数がすべて複素数の中にあることを保証している。
カルダーノが3次および4次方程式の解法を発表したのは、1545年のことであった。5次方程式の解法の不可能性がアーベルによって証明されたのは1824年であり、それまでに実に300年近くもかかった。
しかし、解の置換について最初に考察したのはラグランジュであり、1770年のことだった。アーベルの補題を除けば、解の置換についての上の証明は意外なほどにあっけない。ラグランジュがこのことに気づかなかったのは不思議な気がする。
なお、5次方程式の解法の不可能性を議論するためには、体(field)やベキ根拡大(radical extension)という数学的道具を使う。ただし、アーベルの時代には体の概念は存在しなかったので、アーベルの証明そのものにはこれらの道具は使われていない。
5次方程式の解の公式が存在しないといっても、すべての5次方程式が解けないわけではない。4次以下の多項式に分解できればベキ根と加減乗除で解けるのは当然だが、そうでなくても(既約でも)解ける場合もある。たとえば、
x5 - x4 - 4x3 - 3x2 - 3x - 1 = 0
の解は、
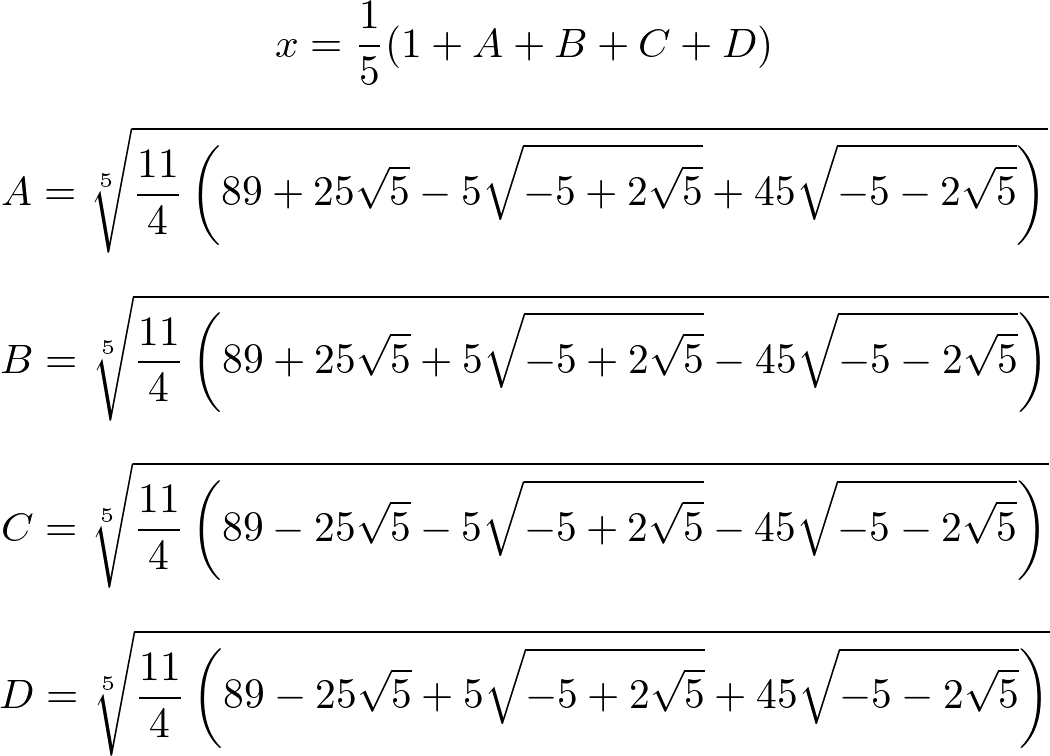
となる!
実はこれは、1の11乗根を ζ としたときの x = -(ζ + 1/ζ) の値である。
1のn乗根は、nがいくつであっても加減乗除とベキ根で表せることがガウスによって証明されている。(17/04/16)
【参考文献】
1.『代数方程式のガロアの理論』Jean-Pierre Tignol、共立出版
2.『群の発見』原田耕一郎、岩波書店
3.『アーベルの証明―「解けない方程式」を解く』Peter Pesic、日本評論社